Q.巨大地震ってどれくらい大きいの?
A.M1.0を1円とすると、M9.0は1兆円に相当します。
■ マグニチュードとは?
まず地震のニュースを思い出して下さい。例えば「午後○時○分頃△△地方を中心に地震がありました。××市の震度は3で、、、地震の規模はマグニチュード4.7でした。」などと報じられます。
この「マグニチュード」と「震度」とは、何でしょう? ニュースを注意して聞くとわかりますが、マグニチュードというのは、地震の規模を表します。震度はある地点の揺れの大きさを表します。 たき火で例えれば、落ち葉を集めた小さなたき火でも、すぐ近くはかなり熱いです。一方、キャンプファイヤーのように、ものすごく大きくな炎でも、遠くに離れると決して熱くはありません。自分が感じる熱さと、たき火の大小は必ずしも同じではありません。このときの、自分の感じる熱さが「震度」であり、たき火の大小が「マグニチュード」にあたります。
たとえ小さな地震(小マグニチュード)でも、震源に近ければ大きく揺れますし、大地震(大マグニチュード)でも震源から遠ければちょっとしか揺れません。
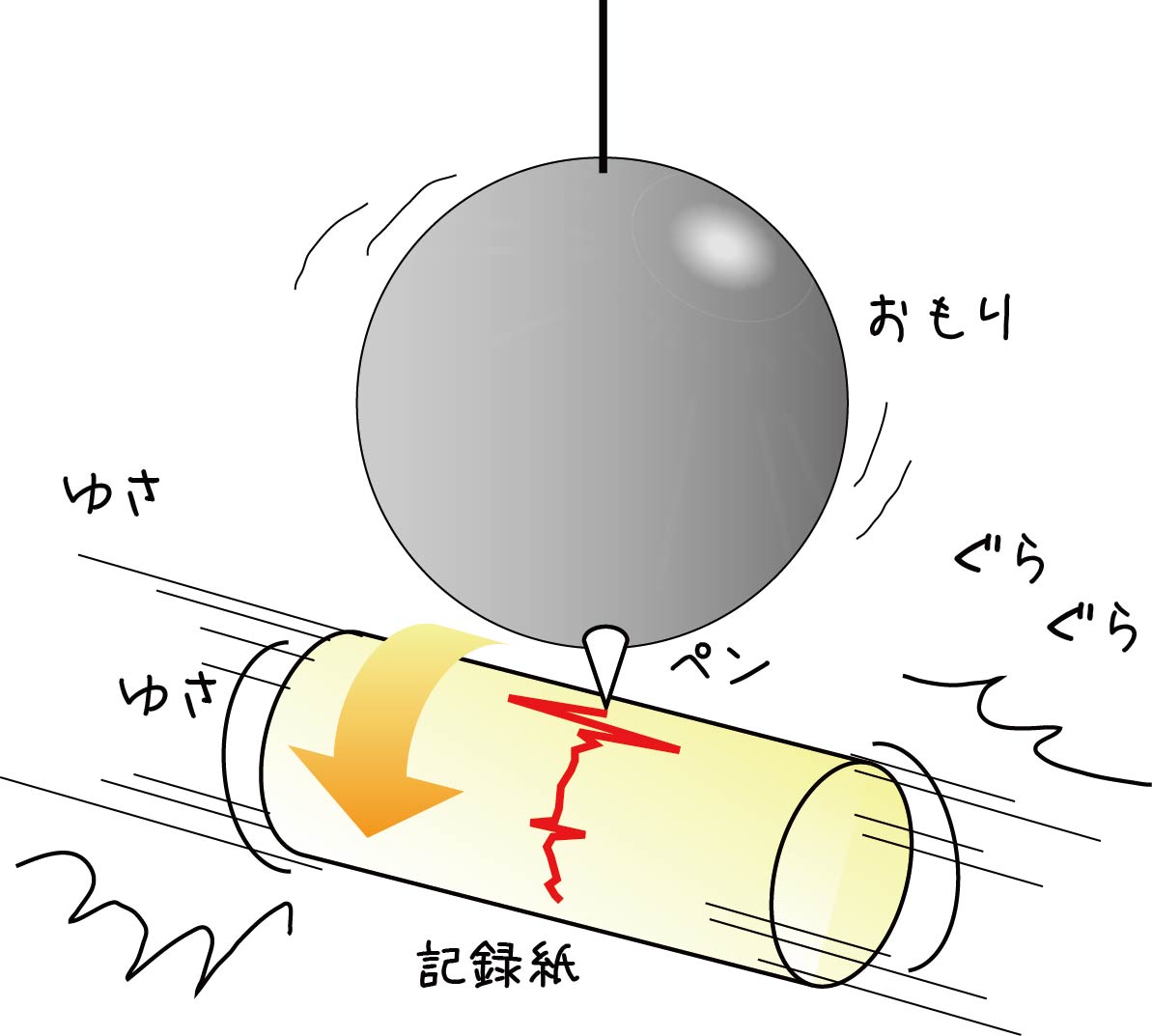
そのため地震の規模を評価するにも距離をそろえて比べる必要があります。古典的な基準では、震源から100kmの位置にある標準地震計の振れ幅を使います。初期の地震計は単純な仕組みで、オモリにペンがついており、地面が揺れてもオモリとペンは慣性の法則で動きません。一方で記録紙は動きます。そのためビヨビヨと波形が記録されます。
この振れ幅からマグニチュード(M)を読み取るのがリヒター・スケール(Richter scale)です。
M =log A + log B
ここでlog Bは地震計と震央の距離の補正値で、100 kmより近ければマイナス、遠ければプラスです。次にlog A、これが重要で地震計の振れ幅をμm (1μm = 0.001 mm)で表したものです。ただしlogですから“桁”がポイントです。ふれ幅を定規で計って、 1 mmだったら 100μmなのでlog Aは3。1000μmなら4です。
つまり振れ幅が 1 mm (100μm)なら M3、 1cm (1000μm)なら M 4、10cm (10000μm) だったらM5 というわけです。「センチやミリといった、オーダーで決っちゃうってこと??」「単純すぎー」と言いたいことでしょう。
しかもこのまま増えていくと、M7だと振れ幅が10m。M9な1kmです。「どんだけでかい記録紙やねん!」 と、つっこみたくなります。 もちろんそんなジャンボ地震計は存在しませんし、そもそも大地が1kmも行ったり戻ったり大きく揺れるなんてあり得ません。ものには限度があります。
単純な揺れ幅による指標では、あまりにも大きな地震は計れないのです。地震の規模を表現するためにマグニチュードが大きな地震には使えないなんて!
もっと良い指標はないだろうか。というわけで登場したのがモーメントマグニチュードです。これは、振れ幅ではなく地震エネルギーで階級を決める新しい指標です。
■ 地震エネルギーって?
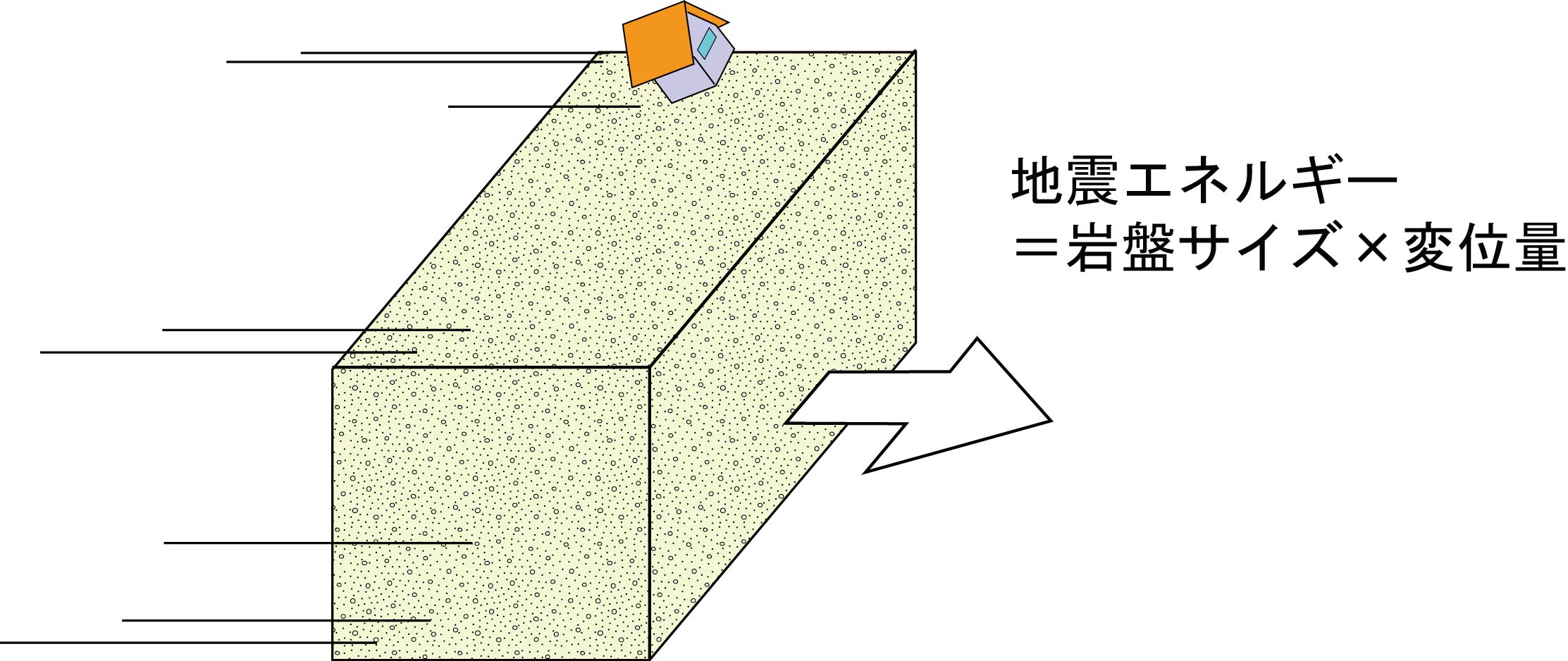
地震エネルギーとは何でしょう? そもそも、地震はどうやって起きるのでしょうか。皆さんにとって「地震=断層が動くこと」であることは、もはや常識だと思います(地震の正体が断層であることが確定したのは70年代であり、実はかなり最新の常識なのです)。
地表では線のように見える断層も、実は地下に広がる地殻内の大きな割れ目であり、これが地震の時にすべります。地震は、巨大な岩盤が断層面沿いにすべる現象なのです。
そのため 岩盤の運動エネルギー=地震エネルギー と言えます。これならば地震の規模を正確に表せそうです。これをモーメントマグニチュード(Mw)と言います。
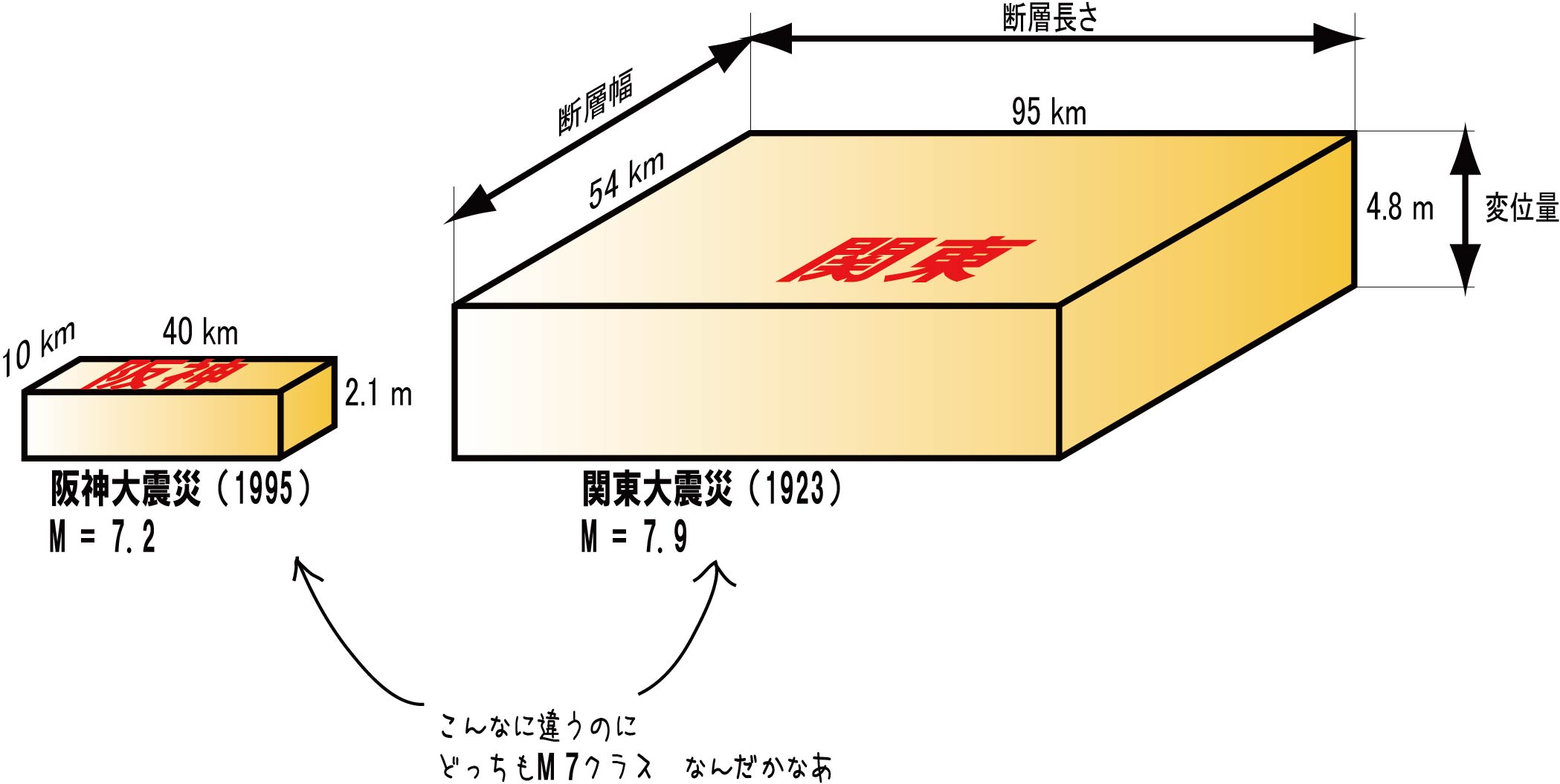
では地震の規模を比較してみましょう。1995年の阪神大震災(Mw:7.2)の断層は、長さ40km、幅10km、変位量2.1mでした。X軸を断層の長さ、Y軸を幅、Z軸を変位量として地震のエネルギーを直方体として表現してみましょう(図1.3)。かの1923年の関東大地震(Mw:7.9)の断層は、長さ130km、幅70km、変位量2.1mです。両方ともマグニチュード7クラスと言うと似たような大きさかと思ってしまいますが、実は全然違います。とんだ誤解でした。関東大地震はスゴイですね。次に1944年12月の東南海地震(Mw:8.0)を見てみると、断層の長さ120km、幅80km、変位量3.1mですから、なんて大きさでしょう! 東南海大地震は恐ろしいものです。
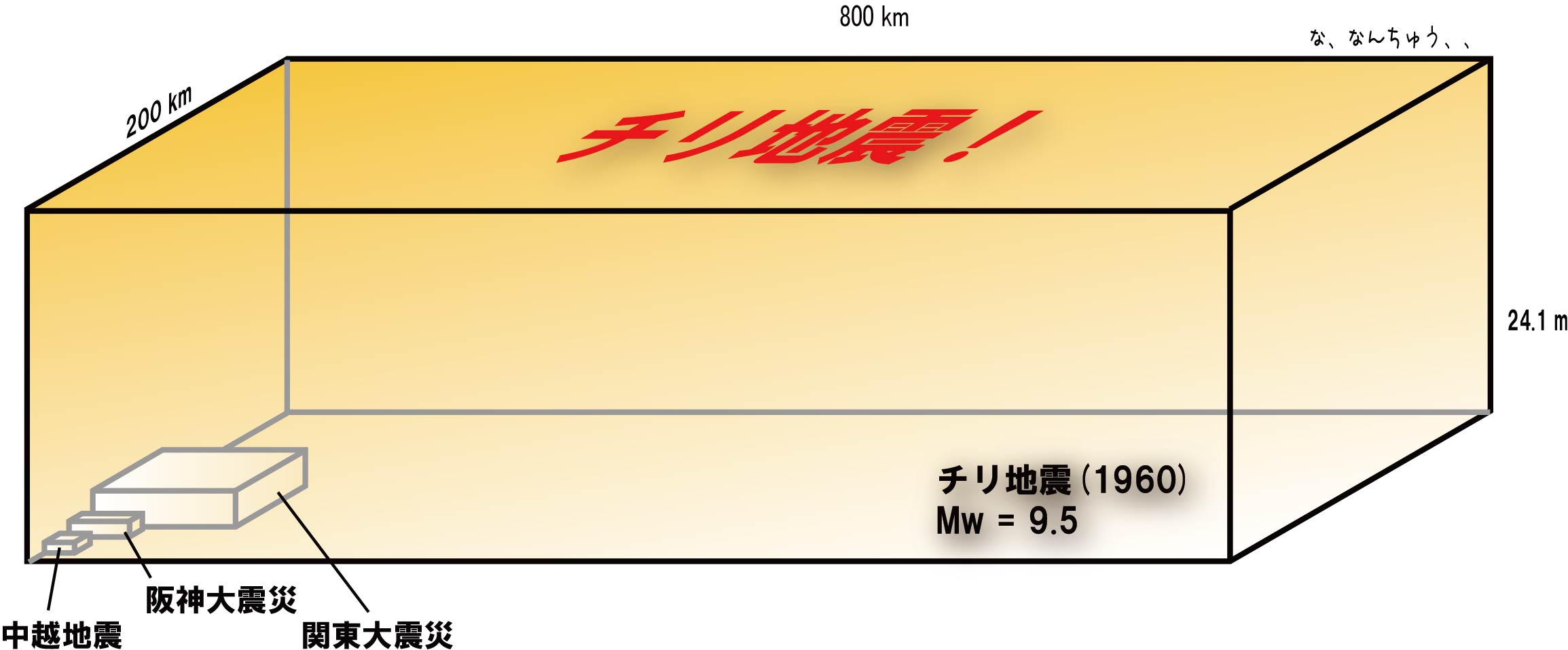
次にM9クラス、世界最大級の地震を見てみましょう。2005年スマトラ島沖地震の断層は、長さ900km、幅150km、変位量10.7mです。2011年の東北地方太平洋沖地震は、断層の長さ450km、幅220km、変位量60m以上です。な、なんとデカイことか! もはや関東大地震や東南海地震すら小さく思えます。まさに桁違いです。そして最後が近代以降の地震観測史上最大の1960年チリ地震(Mw:9.5)です。その断層は、長さ800km、幅200km、変位量40mですから、スマトラ島沖地震よりもはるかに大きいです。桁違いのパワーと迫力。まさにこの惑星最大規模の超巨大地震です。皆さんもぜひノートに描いて、チリ地震のすごさに震撼して下さい。ちなみにこの100年間に地球表層から放出された全地震エネルギーのうち、約1/4近くがたった一回のチリ地震で占められます。つまり地震の世界では、
数回のM9地震 > そのほか全て
という圧倒的寡占状態になっていることがわかります。
| 地震名 | 断層長 | 断層幅 | 変位量 | Mw |
| 阪神大震災(1995年) | 40km | 10km | 2.1m | 6.9 |
| チリ地震(1960年) | 920km | 200km | 40m | 9.5 |
| 東南海地震(1944年) | 140km | 80km | 4.4m | 8.0 |
| 関東地震(1932年) | 95km | 54km | 4.8m | 7.9 |
| 東日本大震災(2011) | 450km | 220km | >60m | 9.0 |
■ まとめ
旧来のマグニチュード(Ms)は特別に大きい地震を評価するのが苦手でした。そのままではチリ地震が8.5になり、東南海地震と同じM8クラスになってしまいます。しかしモーメントマグニチュード(Mw)ならば、チリ地震は 9.5になり、東南海地震の 8.1とは別格であることがちゃんとわかります。
ちなみにマグニチュードが1段階上がると、エネルギーは約32倍も上昇します。そのためM1とM9では1兆倍も差があります。
よく「小さな地震を多数発生させることで巨大地震を解消できないか」という話がでてきますが、それは「1円玉をため続ければ、いつか1兆円の貯金ができる」というのと同じで、簡単ではありません。